What we talk about
when we talk about monads

Tomas Petricek, The Alan Turing Institute
tomasp.net | tomas@tomasp.net | @tomaspetricek

\[\definecolor{mc}{RGB}{137,64,96} \newcommand{\mbnd}{>\!\hspace{-0.25em}>\!\hspace{-0.27em}=}\]

A monad is just a monoid in the category
of endofunctors. What is the problem?

What is a monad?

What do we say when we talk about monads?

Internal history of monads

From category theory to programming

Monads in category theory

A monad over a category \(\mathcal{C}\) is a triple \((T, \eta, \mu)\) where
\(T : \mathcal{C} \rightarrow \mathcal{C}~\) is a functor, \(\eta : {Id}_{\mathcal{C}} \rightarrow T\) and
\(\mu : T^2 \rightarrow T\) are natural transformations such that:

\[\begin{array}{l} \mu_{A} \circ T \mu_A = \mu_{A} \circ \mu_{T A} \\ \mu_{A} \circ \eta_{T A} = \mathit{id}_{T A} = \mu_{A} \circ T \eta_{A} \end{array}\]

Monads in programming

A monad is a triple \((M, \mathit{unit}, \mbnd)\) consisting of a type
constructor \(M\) and two operations of the following types:

\[\begin{array}{lcl} \mbnd &::& M x \rightarrow (x\rightarrow M y) \rightarrow M y\\ \mathit{unit} &::& x\rightarrow M x\\ \end{array}\]

These operations must satisfy the following laws:

\[\begin{array}{l} \mathit{unit}~a~\mbnd~f ~=~ f a\\ m~\mbnd~\mathit{unit} ~=~ m\\ (m~\mbnd~f)~\mbnd~g ~=~ m~\mbnd~(\lambda x.f x~\mbnd~g) \end{array}\]

What has changed?

Explaining monads

Understanding monads using metaphors

Monads as a formal entity

Monad is a data type

Monads as containers

Monad is like a box of things

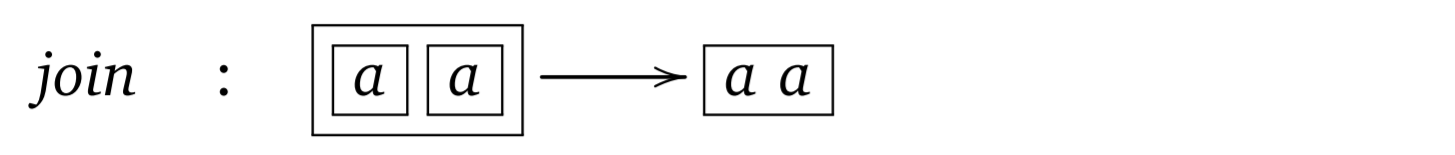
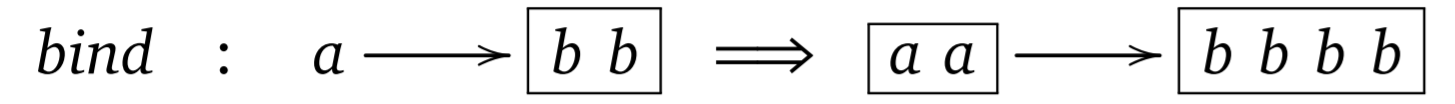
Monads as computations

Monad is like a railway track

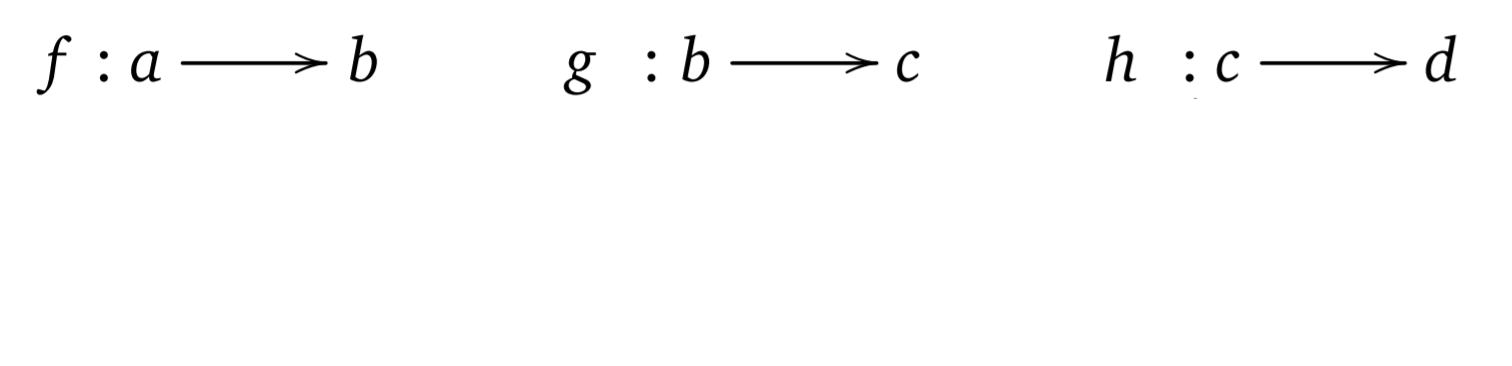
Monads as computations

Monad is like a railway track

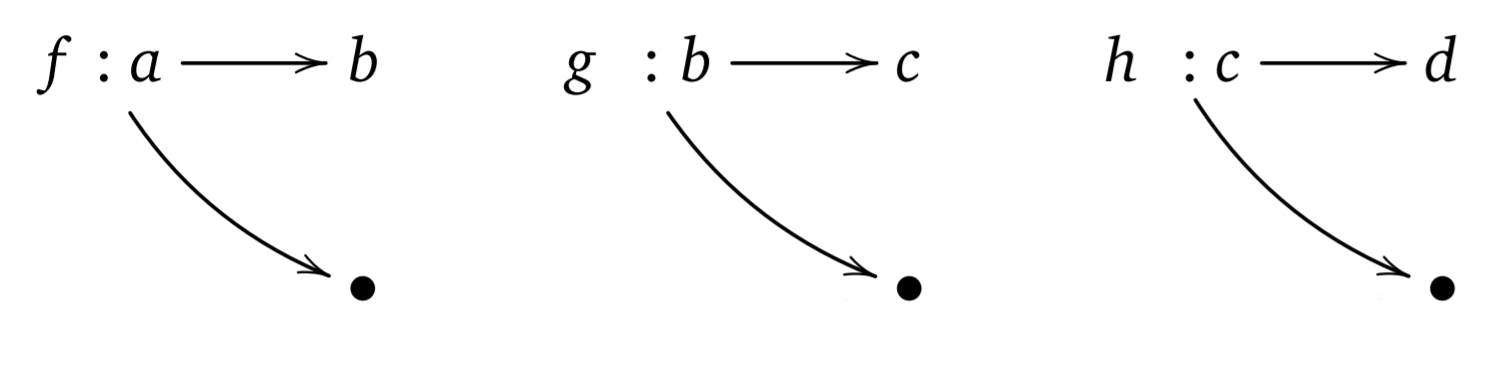
Monads as computations

Monad is like a railway track

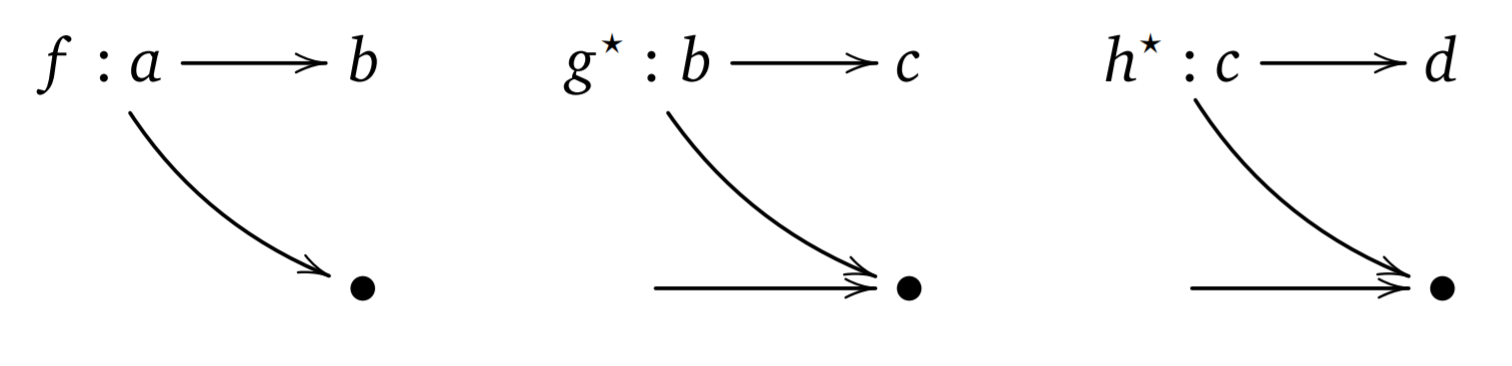
Monads as computations

Monad is like a railway track

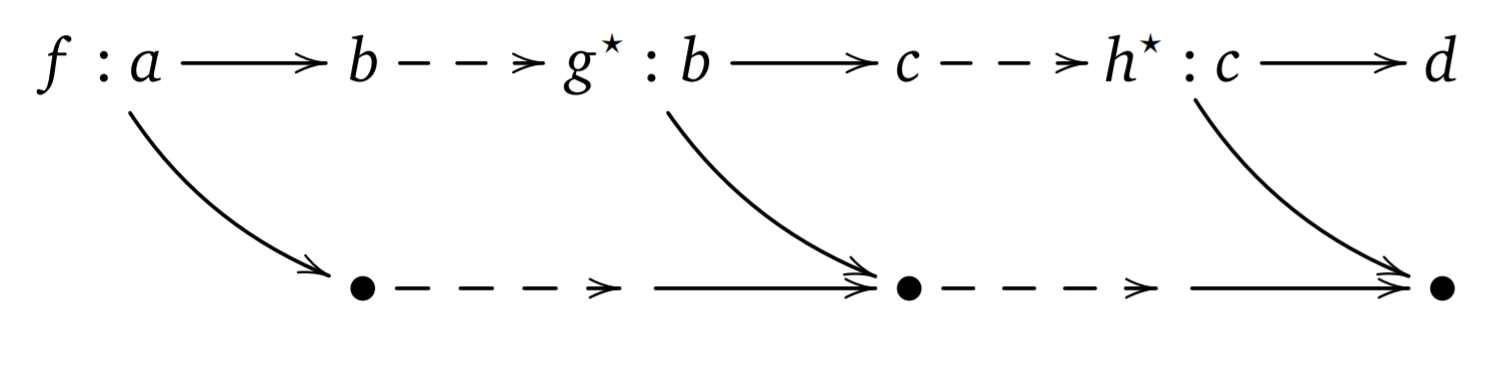
Why metaphors matter

Embodied cognition

Metaphors link abstract concepts with bodily experience

• Movement formal symbol manipulation
• Inside vs. outside for containers and boxes
• Movement for composing railway tracks

Monads in research

Reasoning about programs with monads

This paper is about logics for reasoning about programs,
in particular for proving equivalence of programs.

Moggi (1991)

Origins of algebraic program laws

Intuition about programming constructs

\({\color{mc} \mathit{if}}~\,b~{\color{mc} \mathit{then}}~\,p~{\color{mc} \mathit{else}}~p = p\)

Origins of monad laws

Composition of morphisms in category theory

\((f^\ast \circ g^\ast) \circ h = f^\ast \circ (g^\ast \circ h)\)

\(\mathit{unit}^\ast \circ f = f = f^\ast \circ \mathit{unit}\)

Reasoning about programs with monads

• Monadic query comprehensions (Grust, 2004)
• Monad laws + concrete monads (Gibbons, Hinze, 2011)
• Refactoring using monad laws (To appear... never?)

Algol research paradigm

One of the goals of the Algol programme was to utilize the resources of logic to increase the confidence (...) in the correctness of a program.

(Priestley, 2011)

Monads in programming

From abstractions to syntactic sugar

Code reuse via monadic abstraction

1: 

mapM :: Monad m => (a -> m b) -> [a] -> m [b]        

1: 
2: 
3: 

mapM f x = loop x []
  where loop [] acc = return (reverse acc)
        loop (x:xs) acc = f x >>= \y. loop xs (y:acc)

Sequencing of effects with monads

1: 

main :: IO ()                

1: 
2: 
3: 
4: 

main = do
  putStr "What is your name?"
  n <- readLn
  putStr ("Hello " ++ n)

Non-standard computations

1: 
2: 
3: 
4: 
5: 
6: 

let getLength url = async {
  try
    let! html = downloadAsync url
    return html.Length
  with e ->
    return 0 }

Useful syntactic sugar

1: 

sayHello :: String -> Html 

1: 
2: 
3: 

sayHello name = H.body $ do
  H.header "Welcome"
  H.p ("Hello " ++ name)

How programming concepts evolve

How monads evolve

The nature of programming entities

The nature of programming entities

Metaphorical level

Technical level

Formal level

Shifts and adaptations

Motivation at formal level
Monads are logic for reasoning about effects

Used differently for implementation
Language abstraction for encoding effects

Shift at implementation level
Abstraction and notation for effects

Causes adaptation at metaphorical level
Think of monads as railway tracks

Sociology of monads

Monads as religious objects

Uses of monads

A case for wider understanding

When monads are not the right tool

Monad is a resource of logic

Monad can be the uninteresting part

The Par monad for modelling parallel computations

Monad can be the uninteresting part

Monad as tempting harmful abstraction

Parser a reads input string and produces value a

Monad as tempting harmful abstraction

The normal disadvantages of conventional [monadic] parsers,
such as their lack of speed and their poor error reporting are remedied.

The techniques [do not] extend to monadic parsers. [T]he monadic formu-lation [causes] the evaluation of the parser construction over and over (...).

Swierstra & Duponcheel (1996)

Monad as the wrong structure

Wadge proposed that the semantics of the dataflow language Lucid (...), could be structured by a monad.

Ten years later, Uustalu and Vene gave a semantics for Lucid in terms of a comonad, and stated that "dataflow cannot be structured with monads".

Orchard (2012)

Monad as the wrong structure

• Has the right type of join operation
• Does not provide plumbing

1: 

latest : Stream (Stream a) -> Stream a

Conclusions

What we talk about when we talk about monads

What we talk about when we talk about monads

Strong roots in the Algol paradigm

Meaning evolves at three levels

Metaphors are a fundamental part

Tomas Petricek, The Alan Turing Institute
tomasp.net | tomas@tomasp.net | @tomaspetricek