Not a programming system!?

  • An important part of the ML experience
    Makes ML practical and OCaml efficient
  • Learn some subtle aspects of F# type inference
    Some discovered late through proofs and errors
  • Good example of constraint solving...
    Important technique, used in Prolog & elsewhere

Origins of ML

LCF theorem prover

ML used for writing
meta-programs to generate proofs

Types used to ensure
the validity of proofs

Hindley-Milner

A brief history of type inference

  • Hindley (1969) for Combinatory Logic
  • Milner (1978) for ML with polymorphism
  • Damas (1985) with formal analysis and proofs
  • Since then - type classes, other extensions

Demo

Coeffects playground

Constraint solver
code on GitHub

ML type inference

How does F# figure out the types?

Demo

Basic type inference in F#

How F# type inference works

Constraint-based

  • Collect & solve constraints
  • No annotations needed for ML!

Let polymorphism

  • Infer generic type of let-bound functions

Limitations in ML and F#

  • Value restriction for generic values
  • Harder to deal with .NET objects

Demo

Type inference limitations in F#

TinyHM

A bit of theory

Type systems

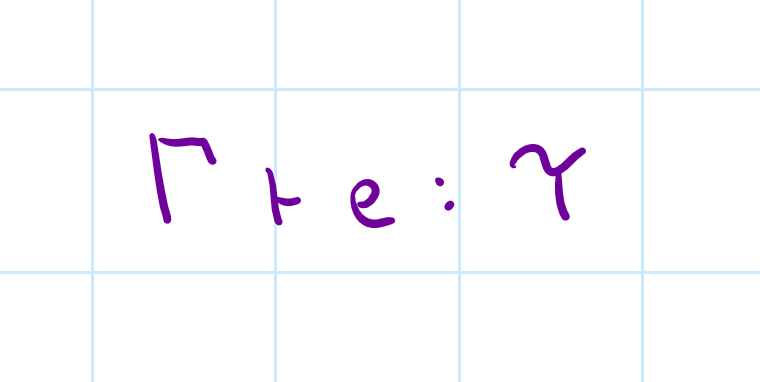
Typing rules

Given a typing context \(\Gamma\), the
expression \(e\) has a type \(\tau\)

The problem in general

We know some of these,
want to figure out the rest

Type systems

Type checking

  • Know it all. Check derivation exists!
  • Easy for syntax-driven rules

Type inference

  • Know expression. Figure out the type!
  • Ideally most general (best) type

Program synthesis

  • Not typical setting, but for completeness...

Principal type (most general)

Best type of
an expression

Any other type of the expression is a special case (subtype) of it

Type inference

  • How Hindely-Milner type inference works?
    Produces most general type (for ML)
  • How Hindely-Milner type inference breaks?
    Nominal types with members, interfaces, etc.
  • Alternative methods for type inference
    Bidirectional - combines checking and inference

TinyHM

Constraint generation & solving

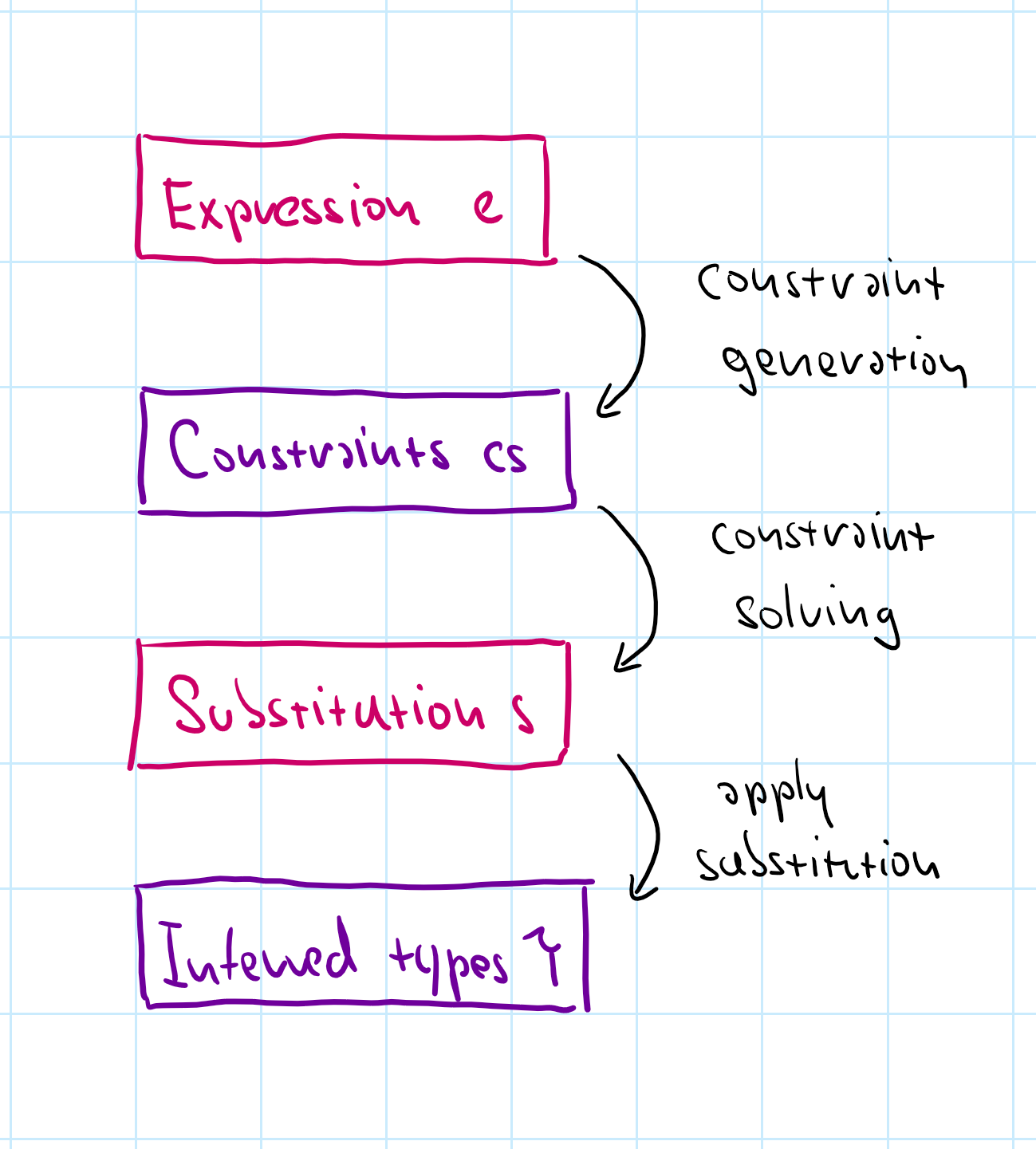
Two phase process

Generate constraints
Recursively over expression

Solve constraints
Recursively over constraint set

In the "Algorithm W", the two are combined. We separate them!

(* Basic types with
   type variables *)
type Type =
  | TyNumber
  | TyVariable of string
  | TyFunction of Type * Type
  | TyList of Type

(* Constraint specifies
   that one type should be
   unified with another *)
type Constraint =
  Type * Type

What is a constraint?

A pair of types that
should be unified

Easy or impossible
int = int -> int
int list = int list

Tricky with variables
'a = int -> 'b
'a = 'c -> int

TinyHM

Constraint generation

  • Generate type and constraints recursively
  • Generate new fresh type variables as needed
  • Variables with new type variables in context
  • Most checking done via constraints

Sketch

Generating constraints

Constraint solver structure

Simplest possible example

  • Peano numbers: Zero, Succ(x)
  • Equality constraints with variables
  • e.g. Succ(x) = Succ(Succ(Zero))

Creating a solver

  • Discharge matching constraints
  • Fail on mismatching constraints
  • Generate more for matching nested
  • Needs to handle substitutions...

Demo

Solving numerical constraints

Remaining work

Substitution (#1) Replace variable in remaining constraints

Substitution (#2)
Apply substitutions
to assigned type

Occurs check (#3) Check for unsolvable constraints

Demo

Substitutions and occurs check

TinyHM

Inference code structure

(* All possible types you may
   support: type variables,
   primitives and composed *)
type Type =
  | TyVariable of string
  | TyBool
  | TyUnit
  | TyNumber
  | TyFunction of Type * Type
  | TyTuple of Type * Type
  | TyUnion of Type * Type
  | TyList of Type
  | TyForall of string * Type

(* Types of known variables *)
type TypingContext =
  Map<string, Type>

Types supported

Type variables
For constraint solving!

Primitive types
Match/mismatch

Composed types
Generate one or two new constraints

Polymorphic type
Forall (bonus)

(* Given a list of
   constraints, produce a
   list of substitutions *)
val solve :
  list<Type * Type>
  -> list<string * Type>

(* Given a typing context
   (known variables) and
   expression, return the type
   of the expression and
   list of constraints *)
val generate :
  TypingContext
  -> Expression
  -> Type * list<Type * Type>

Type inference operations

Constraint solving
Takes constraints
Produces substitution

Constraint generating Takes an expression
Produces constraints
Also check variables

Lab overview

Tiny Hindley-Milner step-by-step

TinyHM - Basic tasks

  1. Complete the simple numerical constraint solver
    Add the two missing substitutions to make it work!

  2. Solving type constraints with numbers and Booleans
    Follow the same structure, but now for type constraints...

  3. Type inference for binary operators and conditionals
    Add constraint generation for a subset of TinyML

  4. Supporting more TinyML expressions
    Add let, functions, application and occurs check

  5. Adding simple data types
    Constraint generation for tuples

TinyHM - Bonus & super tasks

  1. Supporting more TinyML data types
    Add type checking for discriminated unions

  2. Type inference for lists - poor method
    Add recursion & units and try this on list code!

  3. Adding proper support for generic lists
    New type, but without explicit type declarations

  4. Inferring polymorphic code for let bindings
    Implementing proper Hindley-Milner let-polymorphism

  5. Exploring pathological cases
    Did you know HM has DEXPTIME complexity?

Closing

Tiny Hindley-Milner type inference

Conclusions

Tiny Hindley-Milner type inference

  • A remarkable quality of ML language(s)
  • Cannot expect users to write types by hand!
  • Nice introduction to constraint solving
  • Much more can be done with this idea...

Tomáš Petříček, 309 (3rd floor)
petricek@d3s.mff.cuni.cz
https://tomasp.net | @tomaspetricek
https://d3s.mff.cuni.cz/teaching/nprg077