NPRG075

Unexpected perspectives on types

Tomáš Petříček, 309 (3rd floor)
petricek@d3s.mff.cuni.cz
https://tomasp.net | @tomaspetricek

Lectures: Monday 12:20, S7
https://d3s.mff.cuni.cz/teaching/nprg075

Beyond types

Recent developments

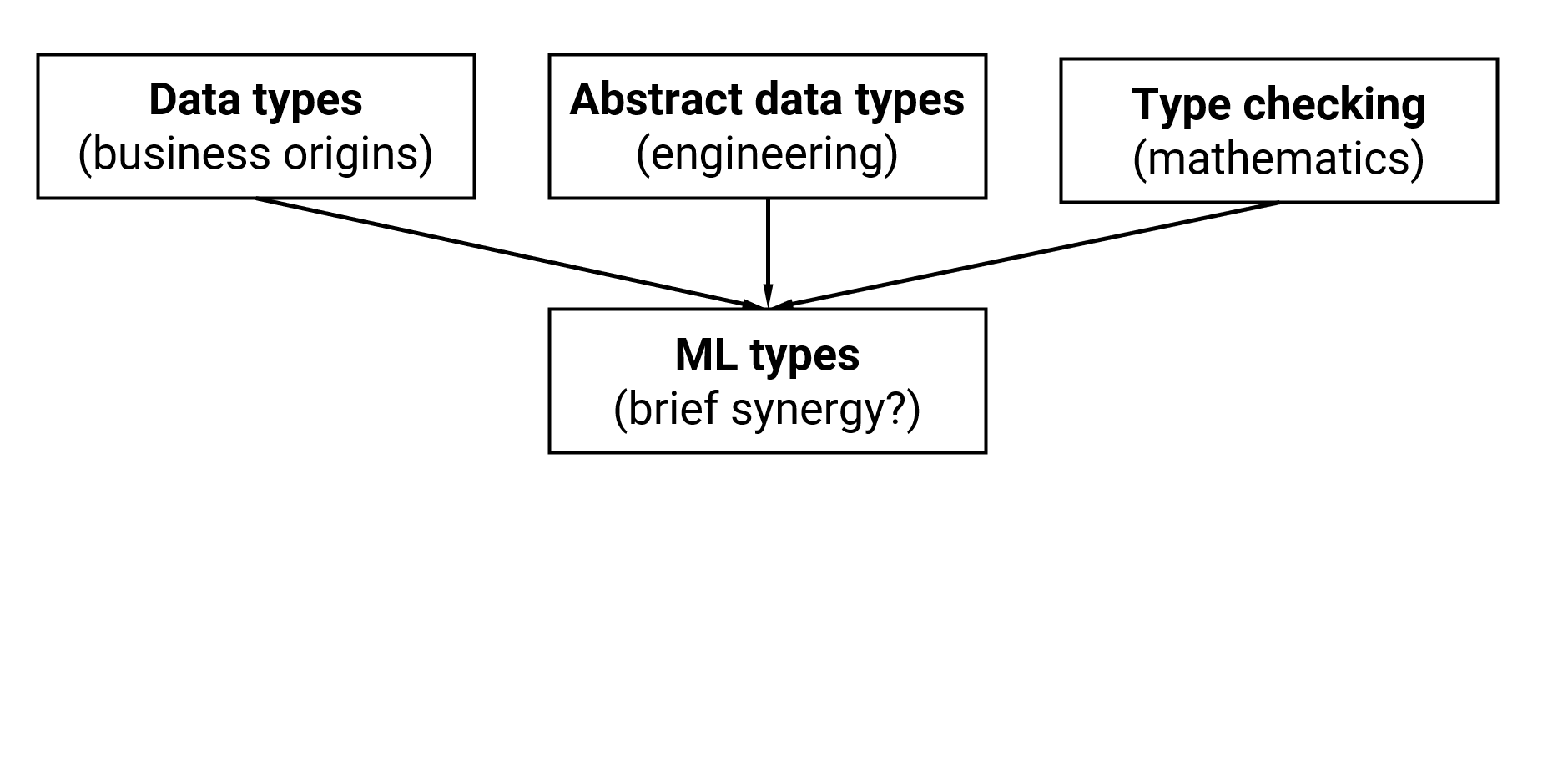
Convergences
and divergences

ML brings together data types, abstract types and checking

End of the history?

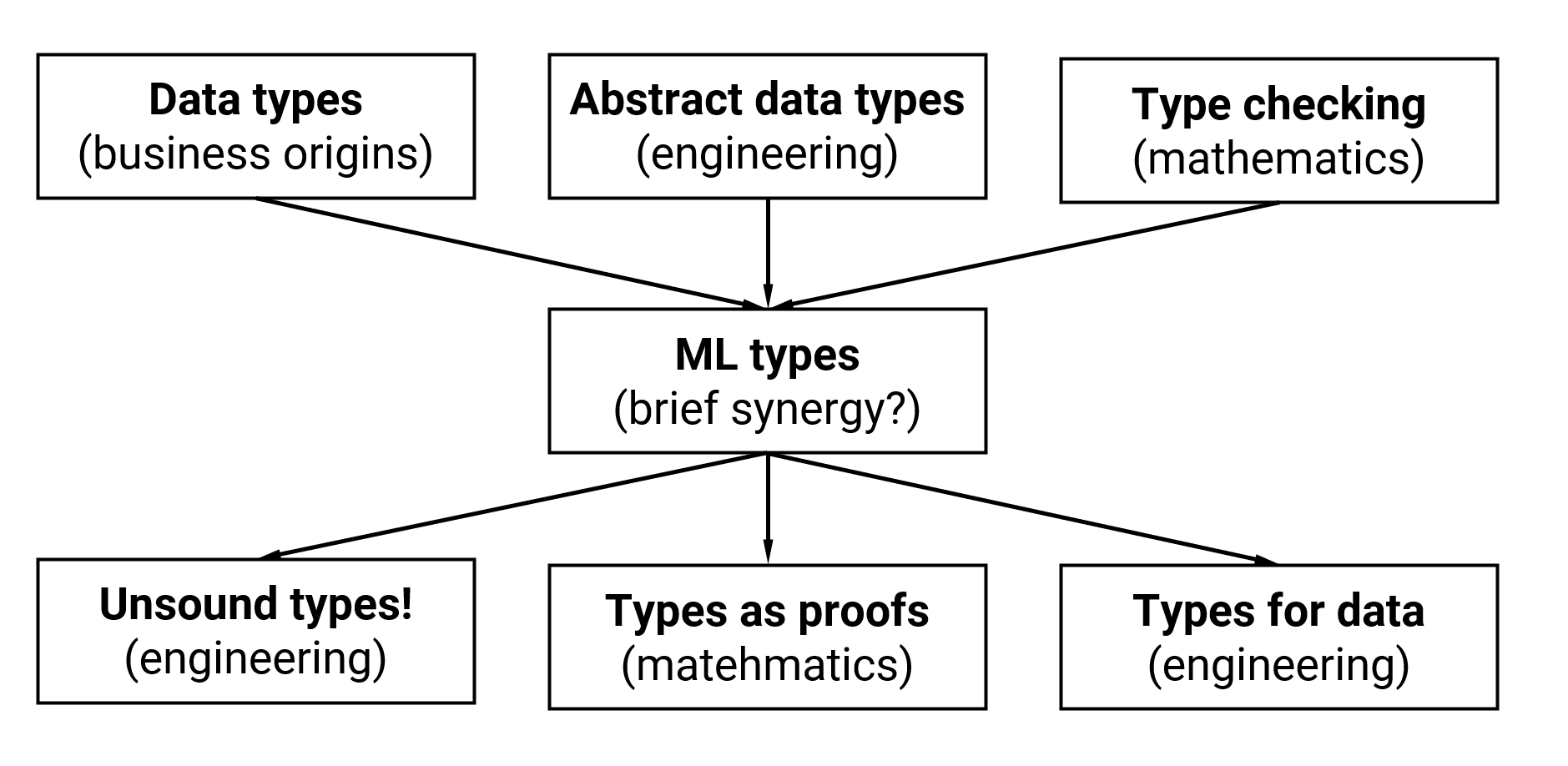
Convergences
and divergences

ML brings together data types, abstract types and checking

End of the history?

Developments in new directions in engineering and mathematics!

Types

Mathematical connections

Types

Mathematical connections

  • Type constructors as algebraic operations
  • Proofs in propositional & predicate logic
  • Linear logic and modal logics
  • Types and cartesian closed categories

Example

Are these two type
definitions equivalent?

type Contact =
  | Email of string
  | Phone of digits
  | Both of string * digits

type Customer =
  { Name : string
    Contact : Contact }

Can one represent some
values the other cannot?

type Option<'T> =
  | Some of 'T
  | None

type Customer =
  { Name : string
    Phone : Option<digits>
    Email : Option<string> }

Calculating with types

Type constructor algebra

  • Record behaves as \(A * B\) or \(A \times B\)
  • Unions behave as \(A + B\) or \(A \cup B\)
  • Functions A->B behave as \(B^A\)
  • Unit type is \(1\) and void (never) is \(0\)

Usual algebraic laws work!

  • \(A*(B+C) = A*B + A*C\)
  • \(A * 1 = A\) and \(A * 0 = 0\)

Calculating with types

\(Contact = (Phone * Email) + Email + Phone\)
\(Customer1\)
\(\quad =Name * Contact\)
\(\quad {\color{green}=Name * ((Phone * Email) + Email + Phone)}\)

\(Customer2\)
\(\quad = Name * (Phone+1) * (Email+1)\)
\(\quad = Name * ((Phone+1) * Email + (Phone+1) * 1)\)
\(\quad = {\color{blue}Name * ((Phone * Email) + Email + Phone }{\color{red}\;+\;1})\)

What else works?

Binary trees

  • Derivative of a binary tree?
  • \(btree = leaf + btree * btree\)
  • Treat \(btree\) as the variable

Derivatives

Derivatives and inverses

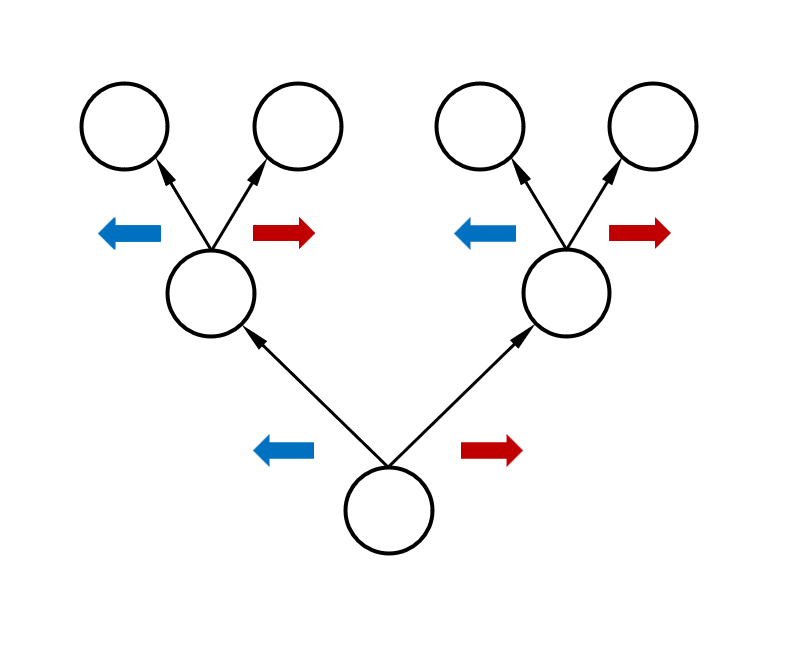
Derivative of a binary tree

  • \(btree = leaf + (btree^2)\)
  • \(btree' = 2*btree\)
  • Steps for iterating over containers
  • Recursively \(2*(2*(2*\ldots))\)

Can define the inverse!

  • Works only in linear logic
  • \(A^{-1} = A \multimap 1\), i.e. a function that consumes a value
  • \((A^{-1} \times A) \multimap 1\), i.e. one direction of equality

Types

Curry-Howard isomorphism

Miraculous link?

Types in programming are propositions in logic!

Programs are proofs!

Not that surprising..

Hard work to make it fit

Same origins in foundations of mathematics

Curry-Hoard isomorphism

Types as propositions

Function \(A\rightarrow B\) corresponds to implication

Product \(A\times B\) corresponds to conjunction \(A \wedge B\)

Union \(A + B\) corresponds to disjunction \(A \vee B\)

Proofs are programs

A well-typed program of type \(A\) is a proof of \(A\)

Write program to show that a property holds!

Theorem provers

Alf, Coq, Agda & more

Construct proofs by interactively creating programs

Show resulting program (Agda) or list of interactions (Coq)

Programs can run too

Programs as proofs

Function composition

Proposition: \(((A \rightarrow B) \wedge (B \rightarrow C)) \rightarrow (A \rightarrow C)\)

Program as proof: \(\lambda (f, g). \lambda a.g (f a)\)

Distributivity

Proposition: \(A \wedge (B \vee C) \rightarrow (A \wedge B) \vee (A \wedge C)\)

Program as proof: \(\lambda (a, \textbf{inl}~b). \textbf{inl}~(a, b)\)
\(~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\; \lambda (a, \textbf{inr}~c). \textbf{inr}~(a, c)\)

Inference rules for types and logic

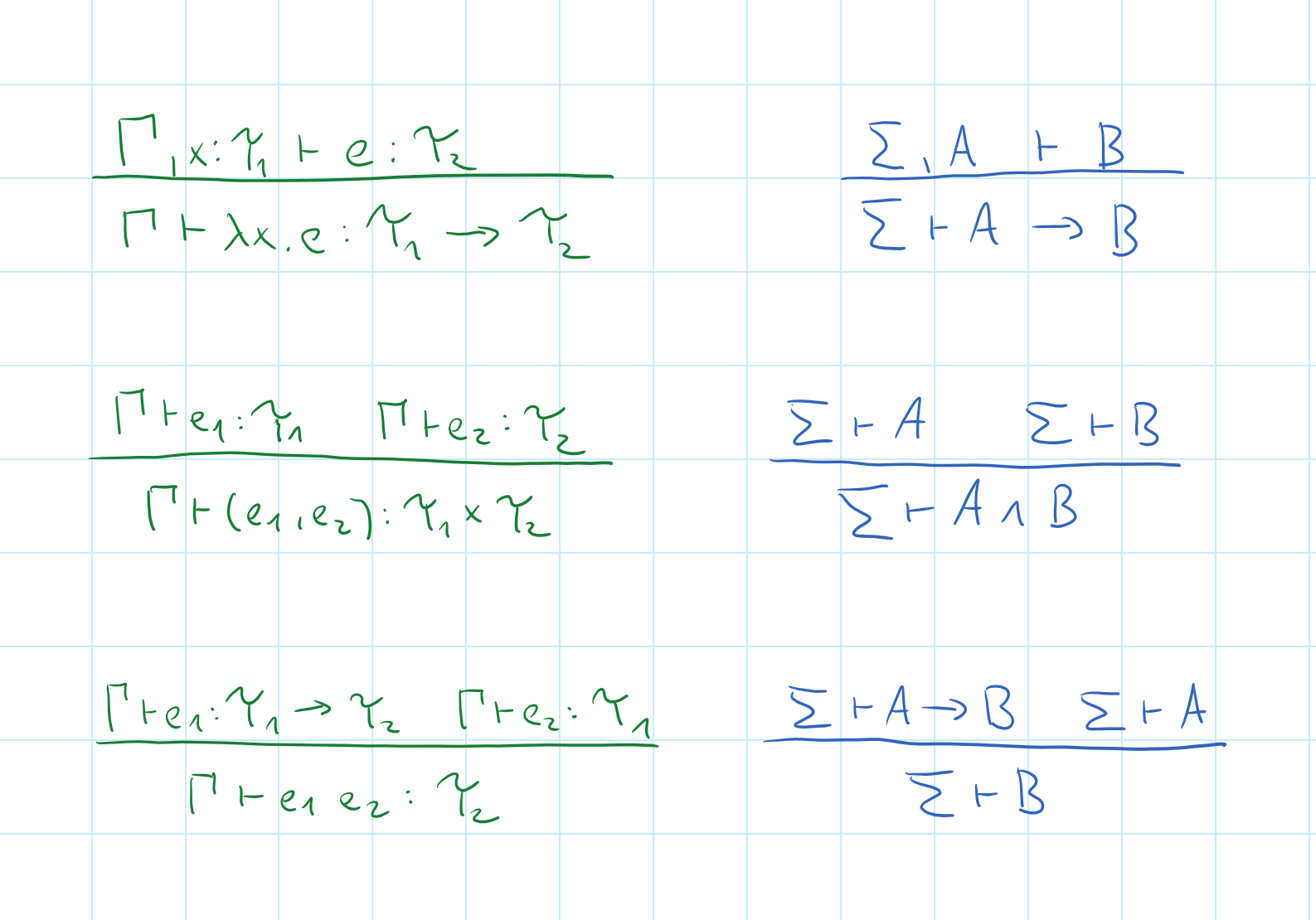
Language design

Importing ideas via maths

  • Simplifying types using algebraic laws
  • Making sense of units and empty types
  • Types inspired by linear and modal logic?
  • Types for universal and existential quantifiers?

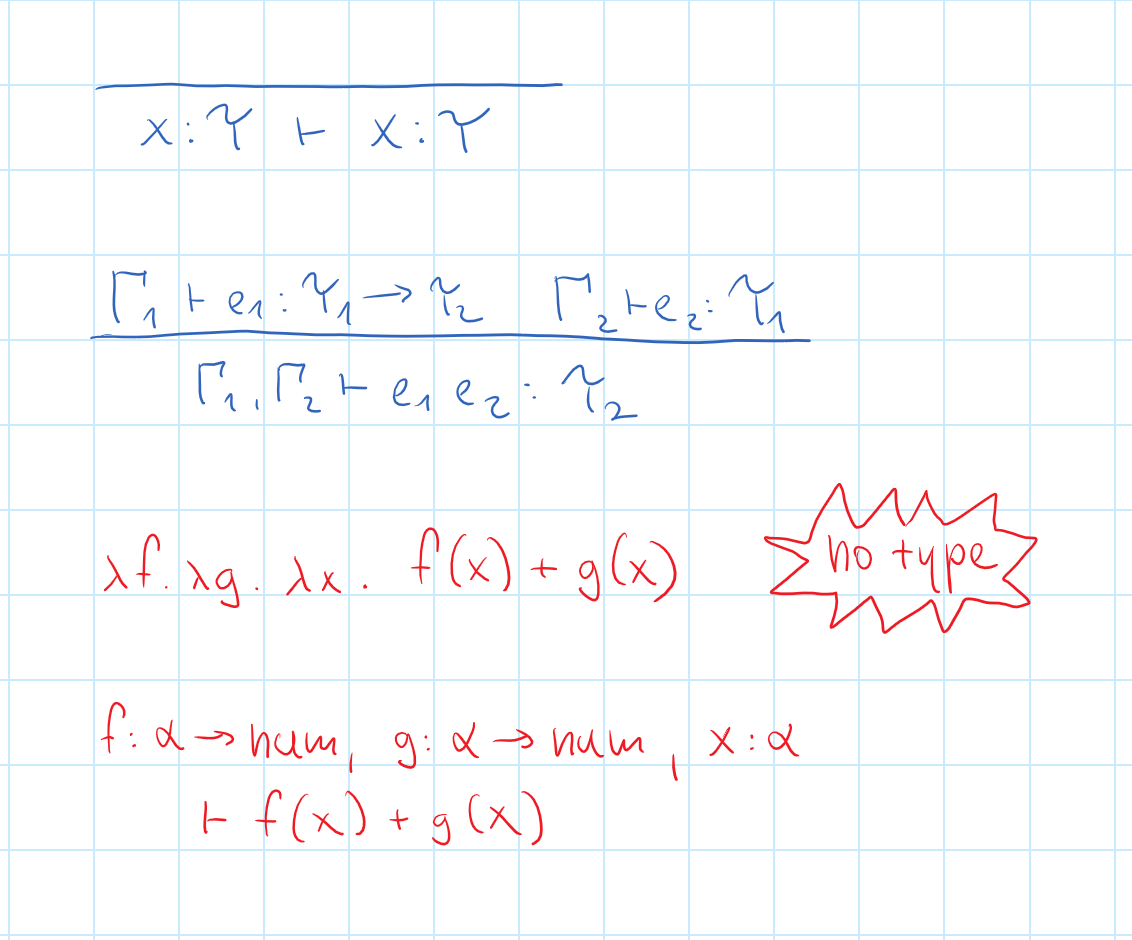
Linear types

Variable must be
used exactly once!

Resource usage in programming!

Avoid aliasing, efficient memory management

Generalizations to control sharing

Types for modal logics

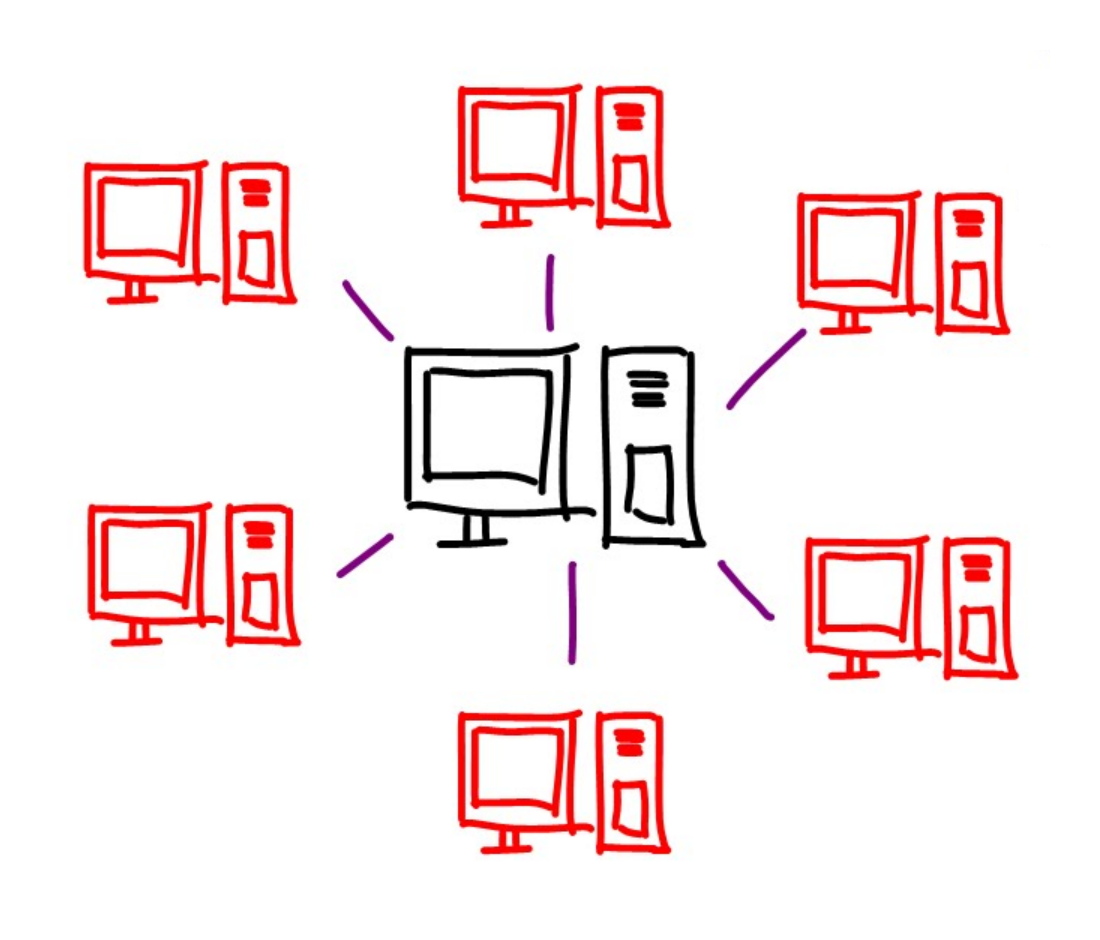
Necessity and possibility

  • \(\diamond A\) - possibility - in a possible world
  • \(\square A\) - necessity - all possible worlds

Distributed systems

  • Value \(A\), address \(\diamond A\), mobile code \(\square A\)
  • Axiom \(\square A \rightarrow A\) - run mobile code to get value
  • Axiom \(A\rightarrow \diamond A\) - take address of local value
  • Axiom \(\diamond A\rightarrow \square\diamond A\) - address is mobile

Dependent types

Quantifiers as type constructors

  • Universal quantification \(\Pi_{x:A}B(x)\)
    Dependent function (x:A) -> B(x)
  • Existential quantification \(\Sigma_{x:A}B(x)\)
    Dependent pair (x:A) * B(x)

Programming languages

  • Origins in theorem provers
  • Dependently-typed languages like Coq, Idris and Agda
  • Some aspects expressible in Haskell, Scala

Using with dependent types

Capture precise information

Vector of a known length Vec (n:int) A
Other properties, like sortedness of a list

Programming with fancy types

Dependent pair and function

vectWithLength : (n:int) * Vec n string
initVector : (x:int) -> (v:A) -> Vec x A

Types

Engineering perspectives

Demo

Checking weather in F#

Type providers

What is a type provider?

  • Extension run at compile-time
  • Can run arbitrary code
  • Generates classes with members

What can they be used for?

  • Infer structure of JSON, XML, CSV
  • Import explicit database schema
  • Interface with a foreign API

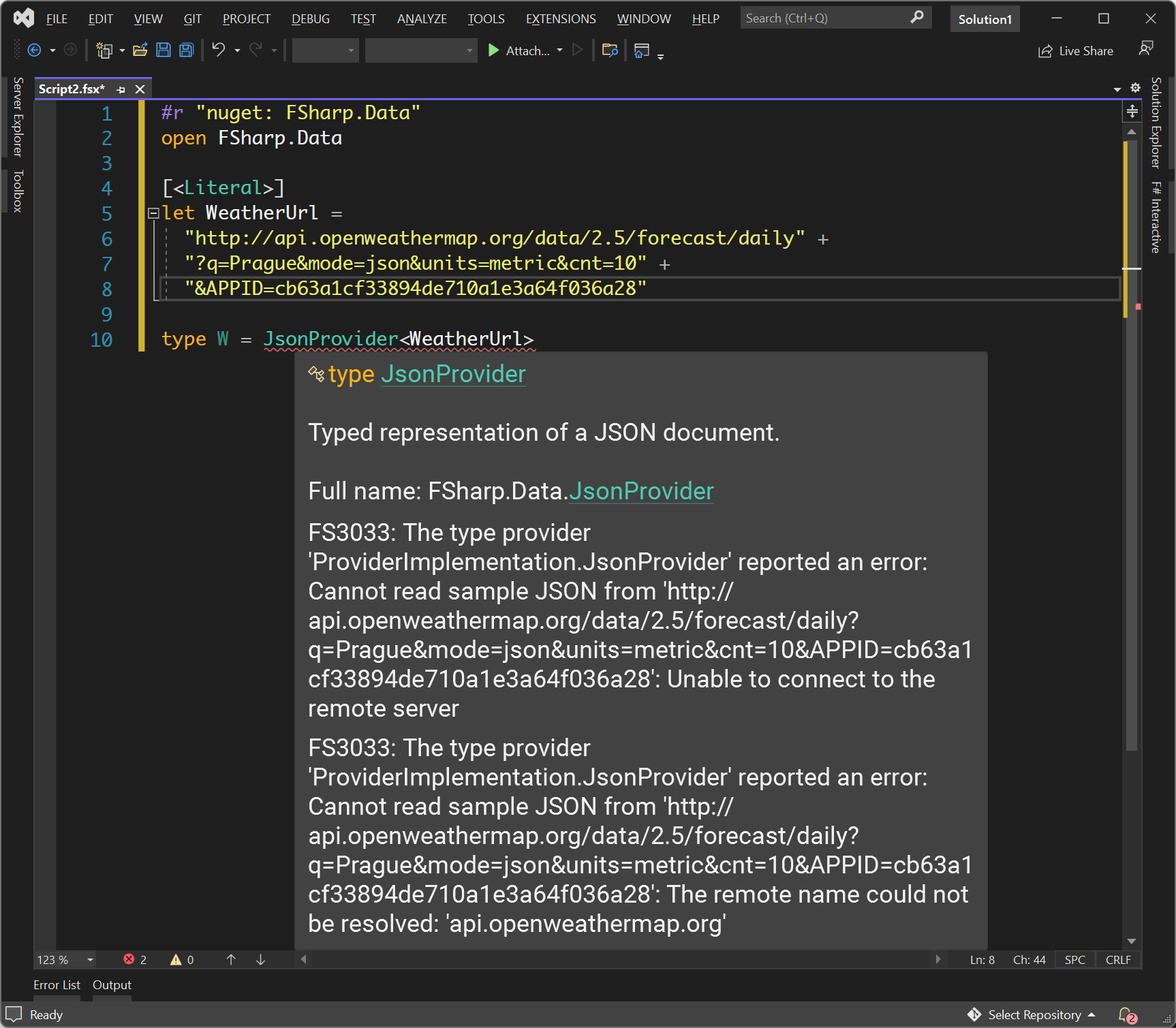
Static type checking?

Type error on a train!

More useful when external service changes format

Well-typed programs
do not go wrong?

Except when the world breaks assumptions
about the schema

Types

Engineering perspective

  • Types have to be useful, not always right
  • Even unsound types help software engineers
  • Invaluable for tooling (completion, checking)
  • Documentation and structuring mechanism

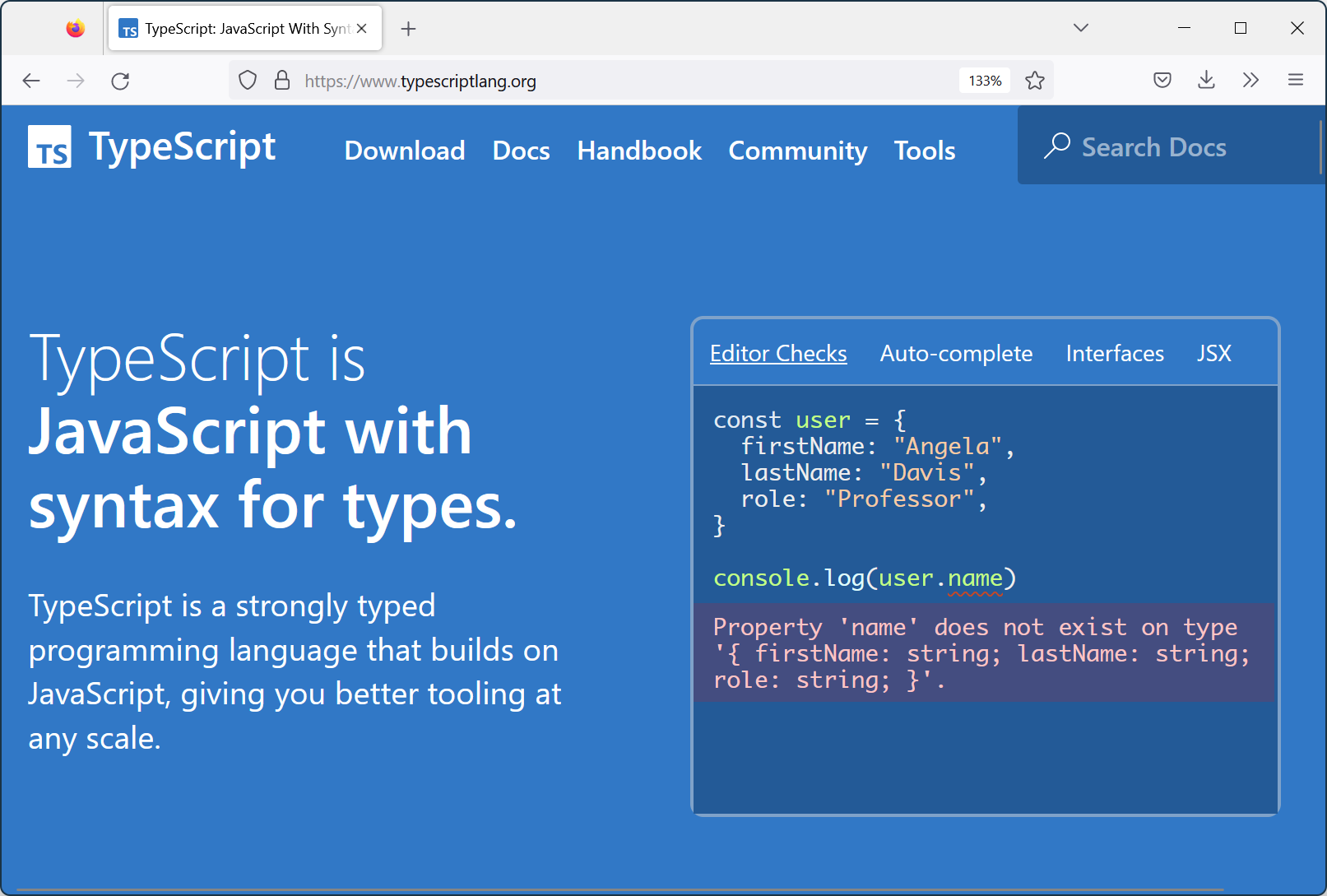
TypeScript types

Unsound because of 'any', covariance, unchecked imports

Checking works
well enough!

More reliable editor auto-completion

Demo

Type providers in The Gamma

The Gamma design

Iterative prompting

  • Do everything via a type provider
  • Construct SQL-like queries & more
  • What are the limits of this?

Type provider tricks

  • Lazy type generation for "big" types
  • Parameterized (dependent) providers
  • Fancy types for the masses

Fancy types for the masses

Row types

\[\frac {\Gamma \vdash e : {\color{red}[f_1:\tau_1, \ldots, f_n:\tau_n]}} {\Gamma \vdash e.\text{drop}~f_i : {\color{cc} [f_1:\tau_1, \ldots, f_{i-1}:\tau_{i-1}, f_{i+1}:\tau_{i+1}, \ldots, f_n:\tau_n]}}\]

Embed as classes

\[\frac {\Gamma \vdash e : {\color{blue} C_1}} {\Gamma \vdash e.\text{drop}~f_i : {\color{blue} C_2}} \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad\]

\[\begin{array}{l} {fields({\color{blue} C_1}) = {\color{blue} \{f_1:\tau_1, \ldots, f_n:\tau_n\}}}\\ {fields({\color{blue} C_2}) = {\color{blue} \{f_1:\tau_1, \ldots, f_{i-1}:\tau_{i-1}, f_{i+1}:\tau_{i+1}, \ldots, f_n:\tau_n\}}} \end{array}\]

Conclusions

Unexpected perspectives on types

Engineering and mathematical views

Complementary ways of designing & evaluating

Import ideas using maths, prove them correct

Adapt ideas for engineering purpose, show they work

Reading

When Technology Became Language: The Origins of the Linguistic Conception of Computer Programming
From davidnofre.com or direct link

What to read and how

  • The birth of programming languages
  • Dramatic change in thinking!
  • Longer, so read what you like...

Conclusions

Unexpected perspectives on types

  • Many ideas imported through mathematics!
  • Dependent, linear and modal types
  • Making it work in practice is a challenge

Tomáš Petříček, 309 (3rd floor)
petricek@d3s.mff.cuni.cz
https://tomasp.net | @tomaspetricek
https://d3s.mff.cuni.cz/teaching/nprg075

References (1/2)

Curry-Howard and dependent types

Type providers & related

References (2/2)

Algebraic types